Intro
Calculating B1 and B0 in Excel is a fundamental concept in regression analysis, which is a statistical method used to establish a relationship between two or more variables. In the context of linear regression, B0 and B1 are coefficients that represent the intercept and slope of the regression line, respectively. Understanding how to calculate these coefficients is essential for interpreting the results of regression analysis and making informed decisions based on data.
The importance of calculating B1 and B0 lies in their ability to help us understand the relationship between variables. For instance, in business, regression analysis can be used to predict sales based on advertising spend, or in finance, to predict stock prices based on historical data. By calculating B1 and B0, we can determine the strength and direction of the relationship between the variables, which can inform strategic decisions.
To calculate B1 and B0 in Excel, you can use the built-in functions and formulas. The most common method involves using the INTERCEPT and SLOPE functions, which directly calculate B0 and B1, respectively. Another approach is to use the LINEST function, which returns an array of coefficients, including B0 and B1, for a linear regression line.
Understanding B0 and B1

Before diving into the calculation methods, it's crucial to understand what B0 and B1 represent. B0, the intercept, is the value of the dependent variable when the independent variable is equal to zero. It essentially tells us the starting point of the regression line. B1, the slope, represents the change in the dependent variable for a one-unit change in the independent variable, while holding all other variables constant. The slope indicates the direction and strength of the relationship between the variables.
Calculating B1 and B0 Using INTERCEPT and SLOPE Functions

The INTERCEPT and SLOPE functions in Excel provide a straightforward way to calculate B0 and B1. The syntax for these functions is as follows:
INTERCEPT(known_y's, known_x's): Returns the intercept of the regression line.SLOPE(known_y's, known_x's): Returns the slope of the regression line.
To use these functions, you need to select the range of cells containing your dependent variable (known_y's) and the range of cells containing your independent variable (known_x's). For example, if your dependent variable data is in cells A1:A10 and your independent variable data is in cells B1:B10, the formula for B0 would be =INTERCEPT(A1:A10, B1:B10), and for B1, it would be =SLOPE(A1:A10, B1:B10).
Calculating B1 and B0 Using the LINEST Function

The LINEST function is another powerful tool in Excel for calculating the coefficients of a linear regression line. The syntax for the LINEST function is:
LINEST(known_y's, known_x's, const, stats): Returns the coefficients of the linear regression line.
When using LINEST, if you set const to TRUE, the function returns B0 as the first element of the array and B1 as the second element. To use LINEST, you need to select a range of cells for the output, enter the formula, and then press Ctrl+Shift+Enter instead of just Enter, because LINEST returns an array.
For example, if your dependent variable data is in cells A1:A10 and your independent variable data is in cells B1:B10, you would select two cells for the output (since we are calculating two coefficients), enter the formula =LINEST(A1:A10, B1:B10, TRUE), and then press Ctrl+Shift+Enter.
Step-by-Step Guide to Using LINEST
1. **Prepare Your Data**: Ensure your dependent and independent variable data are in separate columns. 2. **Select Output Range**: Choose two adjacent cells where you want the coefficients to appear. 3. **Enter the Formula**: Type `=LINEST(known_y's, known_x's, TRUE)`, replacing `known_y's` and `known_x's` with your actual data ranges. 4. **Press Ctrl+Shift+Enter**: This will enter the formula as an array formula.Interpreting B1 and B0

Once you have calculated B1 and B0, interpreting their values is crucial for understanding the relationship between your variables. The slope (B1) indicates how much the dependent variable changes when the independent variable changes by one unit. A positive slope indicates a direct relationship, while a negative slope indicates an inverse relationship. The intercept (B0) provides the baseline value of the dependent variable when the independent variable is zero.
Practical Examples
- **Business**: If you're analyzing the relationship between advertising spend and sales, a positive B1 would indicate that increasing advertising spend leads to an increase in sales. - **Finance**: In predicting stock prices based on historical data, a negative B1 might suggest that as one factor increases, the stock price decreases.Gallery of Regression Analysis
Regression Analysis Image Gallery
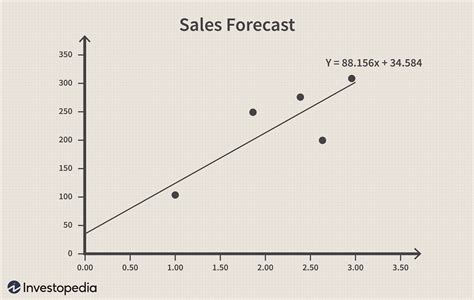



Frequently Asked Questions
What is the purpose of calculating B1 and B0 in regression analysis?
+The purpose of calculating B1 and B0 is to understand the relationship between the dependent and independent variables, including the direction, strength, and the baseline value of the dependent variable.
How do I interpret a positive B1 in regression analysis?
+A positive B1 indicates a direct relationship between the dependent and independent variables, meaning as the independent variable increases, the dependent variable also tends to increase.
What does the intercept (B0) represent in a regression equation?
+The intercept (B0) represents the value of the dependent variable when the independent variable is equal to zero. It provides a baseline value for the dependent variable.
In conclusion, calculating B1 and B0 in Excel is a straightforward process that can be accomplished using the INTERCEPT, SLOPE, and LINEST functions. Understanding these coefficients is crucial for interpreting the results of regression analysis and making informed decisions based on data. By following the steps and examples provided, you can effectively calculate and interpret B1 and B0, enhancing your ability to analyze and predict outcomes in various fields. We invite you to share your experiences with regression analysis and how calculating B1 and B0 has helped you in your projects or research. Your insights can help others deepen their understanding of this powerful statistical tool.