Intro
Calculating the p-value in Excel is a crucial step in statistical hypothesis testing, allowing users to determine the significance of their results. The p-value, or probability value, indicates the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. In this article, we will delve into the importance of p-values, how to calculate them in Excel, and provide practical examples to illustrate the process.
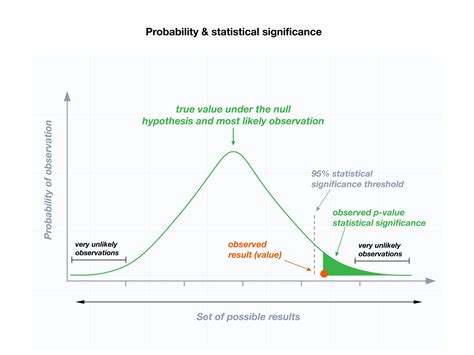
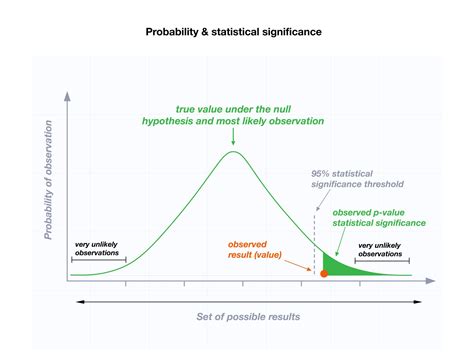
The p-value is a key concept in statistical analysis, as it helps researchers and analysts decide whether their findings are due to chance or if they reflect a real effect. A small p-value (typically less than 0.05) suggests that the observed results are unlikely to occur by chance, leading to the rejection of the null hypothesis. On the other hand, a large p-value indicates that the results could be due to chance, and the null hypothesis cannot be rejected.
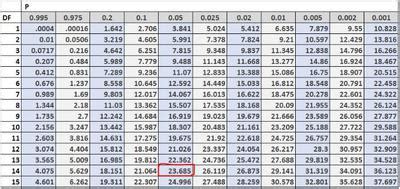
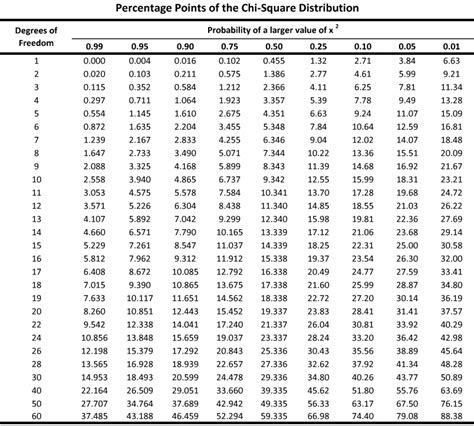
To calculate the p-value in Excel, users can employ various methods, including using built-in functions, such as the T.TEST, Z.TEST, or CHISQ.TEST functions, or by utilizing Excel's Analysis ToolPak add-in. The choice of method depends on the type of test being performed, such as a t-test, z-test, or chi-squared test.
Understanding P-Values

P-values are essential in statistical hypothesis testing, as they provide a measure of the evidence against the null hypothesis. The null hypothesis is a statement of no effect or no difference, while the alternative hypothesis is a statement of an effect or difference. By calculating the p-value, users can determine whether the observed results are consistent with the null hypothesis or if they provide evidence for the alternative hypothesis.
Types of P-Values
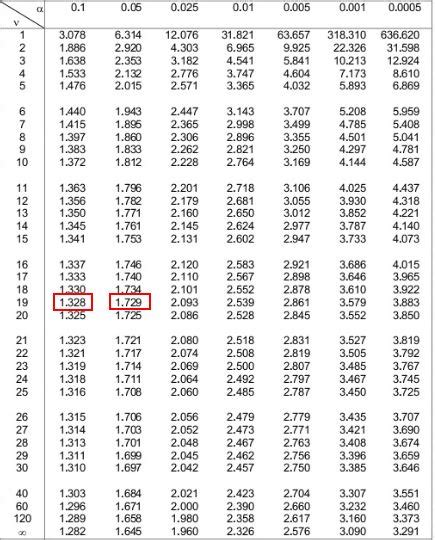
There are two types of p-values: one-tailed and two-tailed. A one-tailed p-value is used when the alternative hypothesis is directional, indicating an increase or decrease in the parameter of interest. A two-tailed p-value is used when the alternative hypothesis is non-directional, indicating an increase or decrease in the parameter of interest, but not specifying the direction.Calculating P-Values in Excel

To calculate p-values in Excel, users can use various built-in functions, such as the T.TEST, Z.TEST, or CHISQ.TEST functions. These functions require input values, such as the sample mean, sample standard deviation, and sample size, to calculate the p-value.
For example, to calculate the p-value for a t-test, users can use the T.TEST function, which has the following syntax: T.TEST(array1, array2, tails, type). The array1 and array2 arguments represent the two samples being compared, the tails argument specifies the number of tails (1 or 2), and the type argument specifies the type of t-test (1 for paired, 2 for two-sample equal variances, or 3 for two-sample unequal variances).
Using the Analysis ToolPak Add-in
The Analysis ToolPak add-in is a built-in Excel add-in that provides a range of statistical tools, including the ability to calculate p-values. To access the Analysis ToolPak, users can go to the Data tab, click on the Data Analysis button, and select the desired statistical tool.Practical Examples
To illustrate the calculation of p-values in Excel, let's consider a few practical examples.
- Example 1: Calculating the p-value for a t-test Suppose we want to compare the means of two samples, A and B. We can use the T.TEST function to calculate the p-value, as follows: =T.TEST(A1:A10, B1:B10, 2, 2), where A1:A10 and B1:B10 represent the two samples, and 2 specifies a two-tailed test.
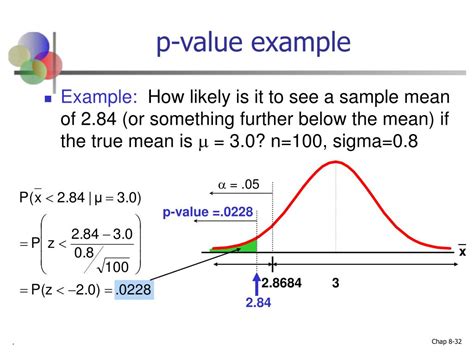
- Example 2: Calculating the p-value for a z-test Suppose we want to compare the mean of a sample to a known population mean. We can use the Z.TEST function to calculate the p-value, as follows: =Z.TEST(A1:A10, 10, 2), where A1:A10 represents the sample, 10 represents the known population mean, and 2 specifies a two-tailed test.
Interpreting P-Values
Once the p-value is calculated, users can interpret the results to determine whether the null hypothesis can be rejected. A small p-value (typically less than 0.05) indicates that the observed results are unlikely to occur by chance, and the null hypothesis can be rejected. A large p-value indicates that the results could be due to chance, and the null hypothesis cannot be rejected.Common Mistakes to Avoid

When calculating p-values in Excel, users should be aware of common mistakes to avoid, such as:
- Incorrectly specifying the number of tails or type of test
- Failing to check for assumptions, such as normality or equal variances
- Misinterpreting the p-value, such as concluding that a significant result is due to the treatment when it may be due to chance
Best Practices
To ensure accurate and reliable results, users should follow best practices, such as:- Checking for assumptions before calculating the p-value
- Using the correct type of test and number of tails
- Interpreting the p-value in the context of the research question and study design
Gallery of P-Value Calculations
P-Value Calculations Image Gallery

Frequently Asked Questions
What is a p-value?
+A p-value is a measure of the evidence against the null hypothesis, indicating the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true.
How do I calculate a p-value in Excel?
+To calculate a p-value in Excel, you can use built-in functions, such as the T.TEST, Z.TEST, or CHISQ.TEST functions, or utilize the Analysis ToolPak add-in.
What is the difference between a one-tailed and two-tailed p-value?
+A one-tailed p-value is used when the alternative hypothesis is directional, while a two-tailed p-value is used when the alternative hypothesis is non-directional.
How do I interpret a p-value?
+A small p-value (typically less than 0.05) indicates that the observed results are unlikely to occur by chance, and the null hypothesis can be rejected. A large p-value indicates that the results could be due to chance, and the null hypothesis cannot be rejected.
What are common mistakes to avoid when calculating p-values?
+Common mistakes to avoid include incorrectly specifying the number of tails or type of test, failing to check for assumptions, and misinterpreting the p-value.
In conclusion, calculating p-values in Excel is a crucial step in statistical hypothesis testing, allowing users to determine the significance of their results. By understanding the importance of p-values, using the correct methods to calculate them, and following best practices, users can ensure accurate and reliable results. We invite you to share your experiences with calculating p-values in Excel, ask questions, or provide feedback on this article.