Nonlinear Regression Analysis Excel

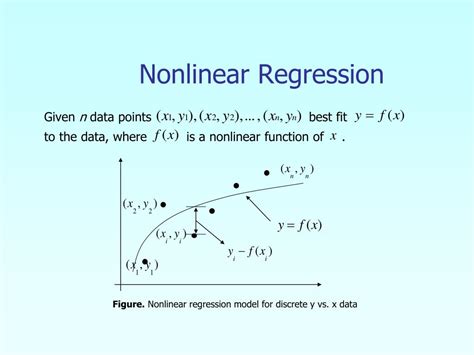
Nonlinear regression analysis is a powerful statistical tool used to model complex relationships between variables. Unlike linear regression, which assumes a straight-line relationship between the independent and dependent variables, nonlinear regression allows for more flexible and accurate modeling of real-world phenomena. In Excel, nonlinear regression analysis can be performed using various methods, including the Solver add-in and third-party software. In this article, we will explore the importance of nonlinear regression analysis, its applications, and how to perform it in Excel.

Nonlinear regression analysis is essential in various fields, such as physics, engineering, biology, and economics, where relationships between variables are often complex and nonlinear. For instance, the relationship between the dose of a drug and its effect on the body is often nonlinear, with the effect increasing rapidly at first and then leveling off. Similarly, the relationship between the temperature and the rate of a chemical reaction is often nonlinear, with the rate increasing exponentially with temperature. By using nonlinear regression analysis, researchers and analysts can better understand these complex relationships and make more accurate predictions.

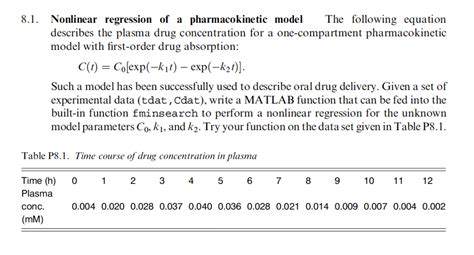
Nonlinear regression analysis has numerous applications in real-world problems. For example, in pharmacokinetics, nonlinear regression is used to model the absorption, distribution, and elimination of drugs in the body. In finance, nonlinear regression is used to model the relationship between stock prices and economic indicators. In environmental science, nonlinear regression is used to model the relationship between pollution levels and environmental factors. By using nonlinear regression analysis, researchers and analysts can identify the underlying patterns and relationships in complex data and make more informed decisions.

Introduction to Nonlinear Regression Analysis

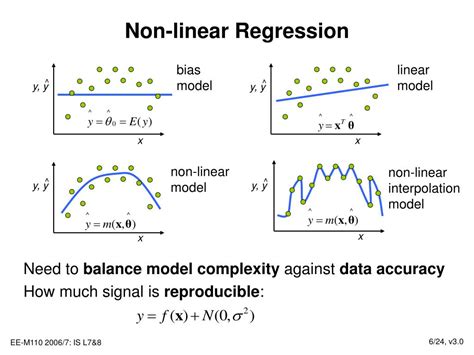
Nonlinear regression analysis is a type of regression analysis where the relationship between the independent and dependent variables is modeled using a nonlinear function. The nonlinear function can take various forms, such as polynomial, exponential, or logarithmic. The goal of nonlinear regression analysis is to find the best-fitting nonlinear function that describes the relationship between the variables. In Excel, nonlinear regression analysis can be performed using the Solver add-in, which is a built-in optimization tool that can be used to find the best-fitting parameters for a nonlinear function.

Types of Nonlinear Regression Analysis

There are several types of nonlinear regression analysis, including: * Polynomial regression: This type of regression analysis uses a polynomial function to model the relationship between the variables. * Exponential regression: This type of regression analysis uses an exponential function to model the relationship between the variables. * Logarithmic regression: This type of regression analysis uses a logarithmic function to model the relationship between the variables. * Logistic regression: This type of regression analysis uses a logistic function to model the relationship between the variables.

Performing Nonlinear Regression Analysis in Excel

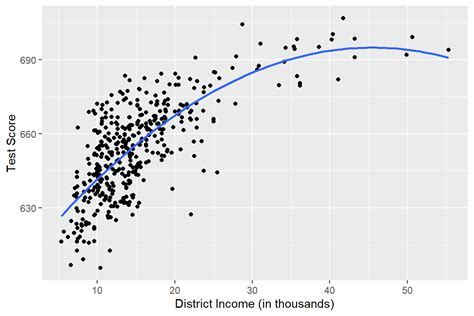
Performing nonlinear regression analysis in Excel involves several steps, including:

1. Preparing the data: The first step is to prepare the data for analysis. This includes cleaning and formatting the data, as well as checking for any missing or outlier values.
2. Choosing a nonlinear function: The next step is to choose a nonlinear function that best describes the relationship between the variables. This can be done by plotting the data and visually inspecting the relationship.
3. Setting up the Solver add-in: Once the nonlinear function has been chosen, the next step is to set up the Solver add-in. This involves defining the parameters of the nonlinear function and specifying the objective function to be minimized.
4. Running the Solver add-in: The final step is to run the Solver add-in and find the best-fitting parameters for the nonlinear function.

Using the Solver Add-in

The Solver add-in is a powerful optimization tool that can be used to find the best-fitting parameters for a nonlinear function. To use the Solver add-in, follow these steps: 1. Go to the Data tab and click on Solver. 2. Define the parameters of the nonlinear function and specify the objective function to be minimized. 3. Click on Solve to run the Solver add-in and find the best-fitting parameters.

Interpreting the Results

Once the Solver add-in has been run, the results can be interpreted. The results include the best-fitting parameters for the nonlinear function, as well as various statistical measures, such as the coefficient of determination (R-squared) and the mean squared error (MSE). These statistical measures can be used to evaluate the goodness of fit of the nonlinear function and to compare the results with other models.

Evaluating the Goodness of Fit

Evaluating the goodness of fit of the nonlinear function is an essential step in nonlinear regression analysis. This can be done by using various statistical measures, such as: * Coefficient of determination (R-squared): This measures the proportion of the variance in the dependent variable that is explained by the nonlinear function. * Mean squared error (MSE): This measures the average squared difference between the observed and predicted values. * Root mean squared error (RMSE): This measures the square root of the average squared difference between the observed and predicted values.

Applications of Nonlinear Regression Analysis

Nonlinear regression analysis has numerous applications in real-world problems. Some of the applications include:

• Pharmacokinetics: Nonlinear regression is used to model the absorption, distribution, and elimination of drugs in the body.
• Finance: Nonlinear regression is used to model the relationship between stock prices and economic indicators.
• Environmental science: Nonlinear regression is used to model the relationship between pollution levels and environmental factors.
• Biology: Nonlinear regression is used to model the growth and development of living organisms.

Real-World Examples

Some real-world examples of nonlinear regression analysis include: * Modeling the relationship between the dose of a drug and its effect on the body. * Modeling the relationship between the temperature and the rate of a chemical reaction. * Modeling the relationship between the concentration of a pollutant and its effect on the environment.

Nonlinear Regression Image Gallery

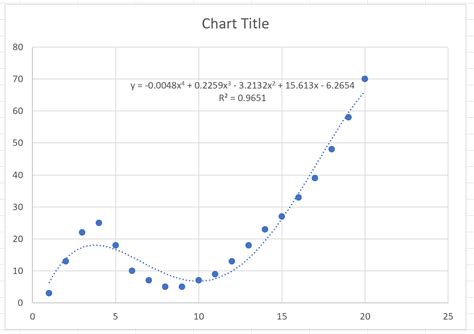
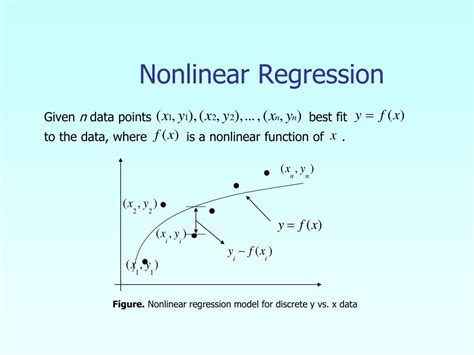
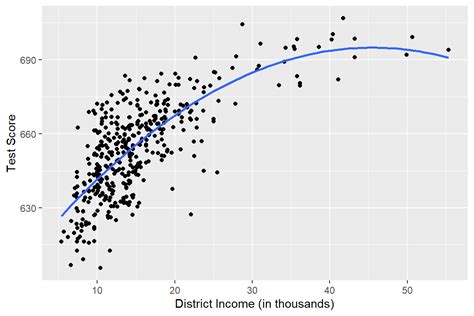
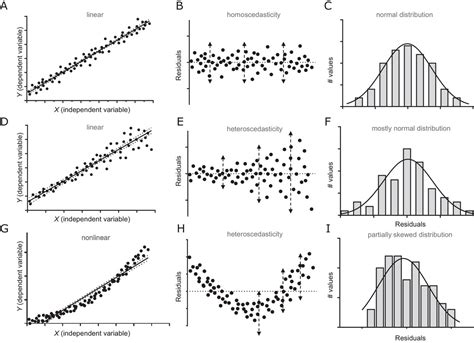
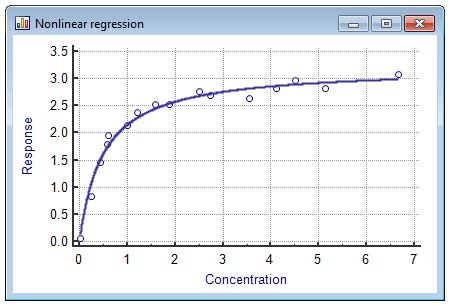
What is nonlinear regression analysis?

+

Nonlinear regression analysis is a type of regression analysis where the relationship between the independent and dependent variables is modeled using a nonlinear function.

How is nonlinear regression analysis performed in Excel?

+

Nonlinear regression analysis can be performed in Excel using the Solver add-in, which is a built-in optimization tool that can be used to find the best-fitting parameters for a nonlinear function.

What are the applications of nonlinear regression analysis?

+

Nonlinear regression analysis has numerous applications in real-world problems, including pharmacokinetics, finance, environmental science, biology, and chemistry.

In conclusion, nonlinear regression analysis is a powerful statistical tool that can be used to model complex relationships between variables. By using the Solver add-in in Excel, researchers and analysts can perform nonlinear regression analysis and find the best-fitting parameters for a nonlinear function. The applications of nonlinear regression analysis are numerous, and it is an essential tool for anyone working with complex data. We hope this article has provided you with a comprehensive understanding of nonlinear regression analysis and its applications. If you have any questions or comments, please feel free to share them with us.