Spearmans Rank Correlation In Excel

The importance of statistical analysis in today's data-driven world cannot be overstated. With the vast amounts of data being generated every day, it's crucial to have tools and techniques that can help make sense of this data. One such technique is correlation analysis, which helps in understanding the relationship between two or more variables. Among various correlation coefficients, Spearman's rank correlation is particularly useful for assessing the relationship between two variables when the data is not normally distributed or when the relationship is not linear. In this article, we will delve into the world of Spearman's rank correlation, its application, and how to calculate it in Excel.

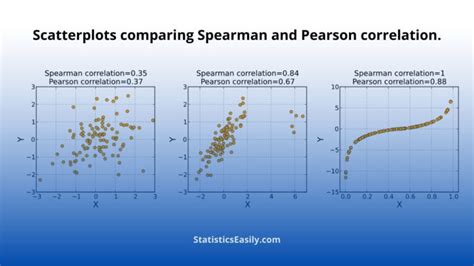
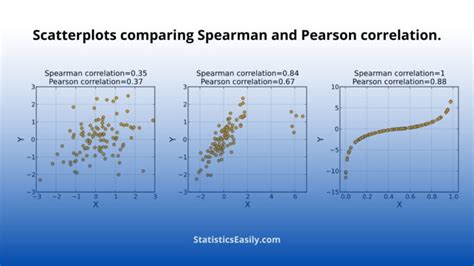
Spearman's rank correlation coefficient is a non-parametric measure that assesses how well the relationship between two variables can be described using a monotonic function. Unlike Pearson's correlation coefficient, which requires the data to be normally distributed and the relationship to be linear, Spearman's rank correlation can handle data that is not normally distributed and can identify non-linear relationships. This makes it a versatile and powerful tool in statistical analysis.

To understand the importance of Spearman's rank correlation, let's consider a scenario where we are analyzing the relationship between the rank of employees based on their performance and the rank based on their salary. If the relationship is perfect, employees ranked higher in performance would also be ranked higher in salary, and vice versa. However, if the relationship is not perfect, Spearman's rank correlation coefficient will provide a value between -1 and 1, indicating the strength and direction of the relationship.

Introduction to Spearman's Rank Correlation

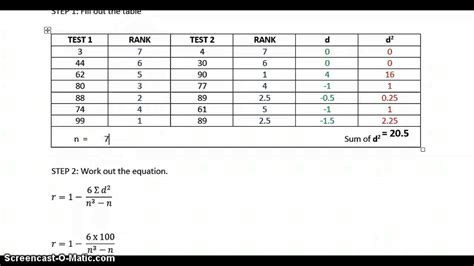
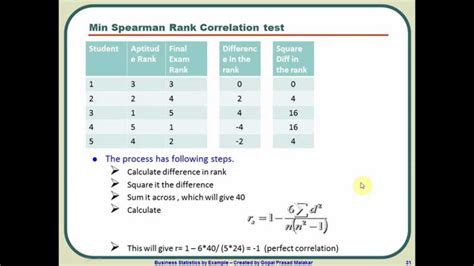
The calculation of Spearman's rank correlation involves ranking the data for each variable and then calculating the correlation coefficient based on these ranks. The formula for Spearman's rank correlation coefficient (ρ) is: ρ = 1 - (6 * Σd^2) / (n^3 - n) where d is the difference in ranks for each pair of observations, and n is the number of observations.

Benefits of Using Spearman's Rank Correlation

The benefits of using Spearman's rank correlation include its ability to handle non-normal data and identify non-linear relationships. It is also less sensitive to outliers compared to Pearson's correlation coefficient. Additionally, Spearman's rank correlation provides a clear and intuitive interpretation of the results, making it easier to understand the strength and direction of the relationship between variables.

Calculating Spearman's Rank Correlation in Excel

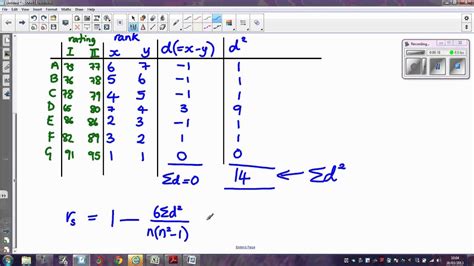
Calculating Spearman's rank correlation in Excel involves several steps:

1. Prepare the data: Ensure that the data is organized in two columns, one for each variable.
2. Rank the data: Use the RANK.AVG function in Excel to rank the data for each variable.
3. Calculate the differences in ranks: Calculate the difference in ranks for each pair of observations.
4. Calculate the sum of squared differences: Calculate the sum of the squared differences in ranks.
5. Calculate the correlation coefficient: Use the formula for Spearman's rank correlation coefficient to calculate the coefficient.

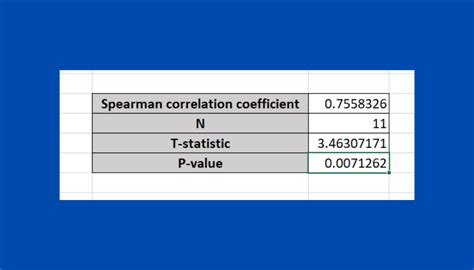
Alternatively, you can use the CORREL function in Excel to calculate the correlation coefficient, and then use the RANK.AVG function to calculate the ranks.

Interpreting the Results

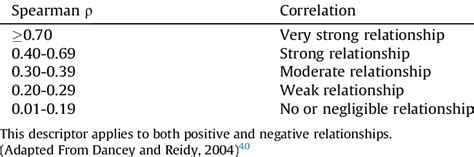
The interpretation of the results involves understanding the value of the correlation coefficient. A value of 1 indicates a perfect positive relationship, a value of -1 indicates a perfect negative relationship, and a value of 0 indicates no relationship. The closer the value is to 1 or -1, the stronger the relationship.

Practical Applications of Spearman's Rank Correlation

Spearman's rank correlation has numerous practical applications in various fields, including:

• Finance: To analyze the relationship between stock prices and trading volumes.
• Marketing: To analyze the relationship between customer satisfaction and loyalty.
• Healthcare: To analyze the relationship between disease symptoms and treatment outcomes.

Common Mistakes to Avoid

Common mistakes to avoid when using Spearman's rank correlation include: * Assuming normality: Spearman's rank correlation does not require normality, but it's essential to check for normality to ensure that the results are valid. * Ignoring outliers: Outliers can affect the results of the analysis, so it's essential to identify and handle outliers before calculating the correlation coefficient. * Misinterpreting the results: The correlation coefficient only indicates the strength and direction of the relationship, not the causality.

Gallery of Spearman's Rank Correlation Images

Spearman's Rank Correlation Image Gallery

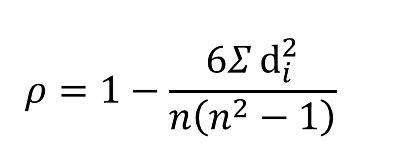
What is Spearman's rank correlation coefficient?

+

Spearman's rank correlation coefficient is a non-parametric measure that assesses how well the relationship between two variables can be described using a monotonic function.

How do I calculate Spearman's rank correlation in Excel?

+

To calculate Spearman's rank correlation in Excel, you can use the RANK.AVG function to rank the data, calculate the differences in ranks, and then use the formula for Spearman's rank correlation coefficient.

What are the benefits of using Spearman's rank correlation?

+

The benefits of using Spearman's rank correlation include its ability to handle non-normal data and identify non-linear relationships, as well as its ease of interpretation.

In conclusion, Spearman's rank correlation is a powerful tool for analyzing the relationship between two variables. Its ability to handle non-normal data and identify non-linear relationships makes it a versatile and valuable technique in statistical analysis. By understanding how to calculate and interpret Spearman's rank correlation, you can gain valuable insights into the relationships between variables and make informed decisions. We invite you to share your thoughts and experiences with Spearman's rank correlation in the comments below, and to share this article with others who may benefit from this knowledge.