Spearmans Rank In Excel

The concept of Spearman's rank correlation is a statistical method used to measure the strength and direction of the relationship between two variables. This method is particularly useful when dealing with data that is not normally distributed or when the relationship between variables is not linear. In the context of Excel, implementing Spearman's rank correlation can be quite straightforward, allowing users to analyze data sets efficiently.

Spearman's rank correlation coefficient, often denoted as ρ (rho), ranges from -1 to 1, where 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation. This coefficient is calculated by ranking the data points for each variable and then computing the correlation between these ranks.

To understand the importance of Spearman's rank correlation in data analysis, it's crucial to recognize its applications. This method is widely used in various fields, including social sciences, medicine, and finance, where the relationship between two variables might not be straightforward. For instance, in psychology, Spearman's rank can be used to correlate the rankings of different personality traits. In finance, it might be used to analyze the relationship between stock prices and trading volumes.

Given its utility, let's delve into how to calculate Spearman's rank correlation in Excel, a popular tool for data analysis. Excel provides several methods to compute Spearman's rank correlation, including using the CORREL function for a basic understanding, though for actual Spearman's rank, one might need to rank data first and then apply the correlation formula.

Understanding the Basics of Spearman's Rank Correlation

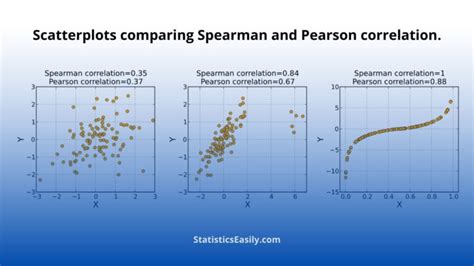
Before diving into the calculation process in Excel, it's essential to understand the concept behind Spearman's rank correlation. This method involves ranking each data point within its respective dataset and then finding the correlation between these ranks. The formula for Spearman's rank correlation coefficient (ρ) is given by: [ \rho = 1 - \frac{6 \sum d^2}{n(n^2 - 1)} ] where (d) is the difference between the ranks of the two variables for each data point, and (n) is the number of data points.

Calculating Spearman's Rank in Excel

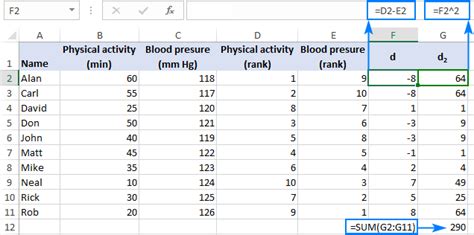
To calculate Spearman's rank correlation in Excel, you can follow these steps:

Prepare Your Data: Ensure your data is organized in two columns, each representing one of the variables you wish to analyze.
Rank Your Data: Use the RANK.AVG function in Excel to rank each data point within its column. The syntax for this function is RANK.AVG(number, ref, [order]), where "number" is the number to rank, "ref" is the reference list, and "[order]" is optional, specifying the ranking order (ascending or descending).
Calculate Differences and Squares: After ranking, calculate the difference between the ranks of corresponding data points in the two columns, then square these differences.
Apply the Spearman Formula: Use the formula mentioned earlier, calculating the sum of the squared differences and applying it to find ρ.

Alternatively, for a more direct approach, especially in newer versions of Excel, you can use the SPEARMAN function from the Analysis ToolPak add-in, which directly calculates the Spearman rank correlation coefficient.

Practical Example in Excel

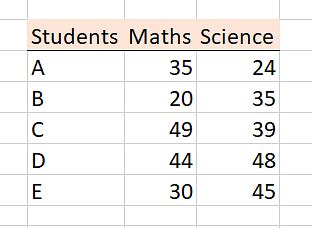
Let's consider a practical example where we have two sets of exam scores for a group of students, and we want to find the Spearman's rank correlation between these scores.

Enter Data: Input the scores in two separate columns in Excel.
Rank Scores: Use the RANK.AVG function to rank the scores in each column.
Calculate Differences and Squares: Compute the differences in ranks and square them.
Calculate Spearman's ρ: Apply the Spearman's rank correlation formula.

This process gives you a clear, step-by-step method to analyze the relationship between two variables using Spearman's rank correlation in Excel.

Interpreting Spearman's Rank Correlation Coefficient

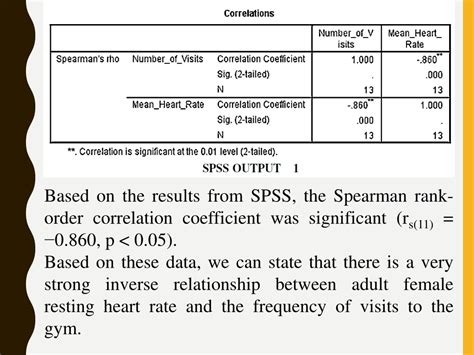
Interpreting the Spearman's rank correlation coefficient (ρ) involves understanding its value, which ranges from -1 to 1.

A value of 1 indicates a perfect positive correlation between the ranks of the two variables.
A value of -1 indicates a perfect negative correlation.
A value close to 0 suggests little to no correlation.

The interpretation of the coefficient's absolute value can be generalized as follows:

0.00 to 0.30: Little or no correlation
0.30 to 0.50: Low correlation
0.50 to 0.70: Moderate correlation
0.70 to 0.90: High correlation
0.90 to 1.00: Very high correlation

Gallery of Spearman's Rank Correlation Examples

Spearman's Rank Correlation Image Gallery

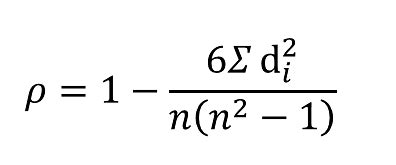
Frequently Asked Questions

What is Spearman's Rank Correlation?

Spearman's rank correlation is a statistical method used to measure the strength and direction of the relationship between two variables based on their ranks.

How is Spearman's Rank Correlation Calculated in Excel?

It can be calculated by ranking data points, finding the differences in ranks, squaring these differences, and applying the Spearman's rank correlation formula, or by using the SPEARMAN function in the Analysis ToolPak add-in.

What Does the Spearman's Rank Correlation Coefficient Value Mean?

The coefficient value ranges from -1 to 1, indicating the strength and direction of the correlation between the two variables, with 1 being a perfect positive correlation, -1 being a perfect negative correlation, and 0 indicating no correlation.

In conclusion, Spearman's rank correlation is a valuable statistical tool for analyzing the relationship between two variables, especially when the data does not follow a normal distribution or when the relationship is not linear. Excel provides a straightforward method to calculate this correlation, making it accessible for data analysis. Understanding and interpreting the Spearman's rank correlation coefficient can provide insights into the nature of the relationship between variables, which is crucial in various fields of study and professional applications. If you have any further questions or need more detailed explanations on specific steps, feel free to ask in the comments below. Share this article with others who might benefit from learning about Spearman's rank correlation in Excel.